Place anonymous order and get professional help from academic writers.
Fast turnaround and high quality guarantees. Available 24/7.
250 000+ happy customers.

Confidential orders and secure payments. 100% privacy is granted.

Top-grade academic writing in compliance with instructions.

Fast and timely delivery, starting at 3 hours. No missed deadlines.

16 years of experience and 50000+ positive reviews.

First, we expect our future author to have a University degree and at least 2 years of expertise in custom writing. All applicants for the writer’s position must meet these requirements. Otherwise, we turn down the candidate right away.
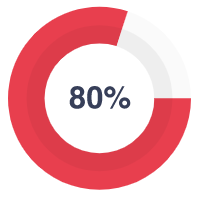
The next stage is an English language test and subject proficiency assessment. Excellent knowledge in the study area is another essential requirement to join our team. 80% of candidates pass the exam successfully.
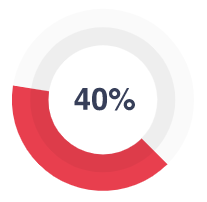
A good essay writer is a qualified professional with the necessary hard and soft skills. A one-on-one meeting allows us to find flexible and outgoing authors with great time-management qualities and a genuine passion for writing.
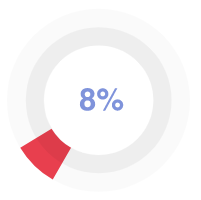
As a final proof-test, the remaining candidates have to complete a guest assignment to show their competence and ability to cope with real orders. Only 8% perform the best and complete a top-quality custom paper.





College essay writing. The essay is the most common written assignment at college. Tell us ‘write my essay online,’ specify your subject and topic, and receive a compelling English essay within your deadline.
Research essay writing. This assignment is one of the most challenging because it requires in-depth academic research. Our writers have access to up-to-date, relevant sources and can create outstanding research essay on any topic.
English essay writing. This service is popular among international students. If English is not your first language, writing a good college essay is extremely difficult. Buy essay online and get a higher grade without effort.
Dissertation writing service. Request dissertation help, and we will find an eligible writer with a PhD degree in your field to create an outstanding dissertation just for you.
Editing service. If you have already written your paper but need another pair of eyes to look at it, try our editing service. A professional academic editor will go over your paper and master it to absolute perfection.

Onlineacademicpaperhelp.com helps students cope with college assignments and write papers on a wide range of topics. We deal with academic writing, creative writing, and non-word assignments.
All of papers you get at Onlineacademicpaperhelp.com are meant for research purposes only. The papers are not supposed to be submitted for academic credit.
Copyright @ 2004 – 2023, Onlineacademicpaperhelp.com. All rights reserved
Call: +1 (563) 635-3236
Support@Onlineacademicpaperhelp.com
Online Chat 24/7